Management frequency and extinction risk
GMSE: an R package for generalised management strategy evaluation (Supporting Information 6)
A. Bradley Duthie¹³, Jeremy J. Cusack¹, Isabel L.
Jones¹, Jeroen Minderman¹,
Erlend B. Nilsen², Rocío A. Pozo¹, O. Sarobidy Rakotonarivo¹,
Bram Van Moorter², and Nils Bunnefeld¹
Erlend B. Nilsen², Rocío A. Pozo¹, O. Sarobidy Rakotonarivo¹,
Bram Van Moorter², and Nils Bunnefeld¹
[1] Biological and Environmental Sciences, University of Stirling, Stirling, UK [2] Norwegian Institute for Nature Research, Trondheim, Norway [3] alexander.duthie@stir.ac.uk
Source:vignettes/SI6.Rmd
SI6.RmdThe individual-based approach of default GMSE sub-models
The default sub-models of GMSE (resource,
observation, manager, user) are
individual-based (also called ‘agent-based’), meaning that they model
discrete individuals (resources or agents), which in GMSE are
represented by individual table rows (as in RESOURCES,
AGENTS, and OBSERVATION) or layers of
three-dimensional arrays (as in COST and
ACTION). Individual-based models (IBMs) have been a useful
approach in ecology for decades (Uchmański and Grimm
1996; Grimm
1999), providing both a pragmatic tool for the mechanistic
modelling of complex populations and a powerful technique for
theoretical investigation. A key advantage of the individual-based
modelling approach is the discrete nature of individuals, which allows
for detailed trait variation and complex interactions among individuals.
In GMSE, some of the most important traits for resources include types,
ages, demographic parameter values, locations, etc., and for agents
(manager and users), traits include different types, utilities, budgets,
etc. The traits that resources and managers have can potentially affect
their interactions, and default GMSE sub-models take advantage of this
by simulating interactions explicitly on a landscape (see Default GMSE data structures for an introduction to
GMSE default data structures).
Replicate simulations as a tool for model inference
Mechanistically modelling complex interactions among discrete
individuals typically causes some degree of stochasticity in IBMs (in
the code, this is caused by the sampling of random values, which
determine probabilistically whether or not events such as birth or death
occur for individuals), reflecting the uncertainty that is inherent to
complex systems. We can see a simple example of this by calling
gmse_apply under the same default conditions twice.
rand_eg_1 <- gmse_apply();
print(rand_eg_1);## $resource_results
## [1] 1109
##
## $observation_results
## [1] 748.2993
##
## $manager_results
## resource_type scaring culling castration feeding help_offspring
## policy_1 1 NA 69 NA NA NA
##
## $user_results
## resource_type scaring culling castration feeding help_offspring
## Manager 1 NA 0 NA NA NA
## user_1 1 NA 14 NA NA NA
## user_2 1 NA 14 NA NA NA
## user_3 1 NA 14 NA NA NA
## user_4 1 NA 14 NA NA NA
## tend_crops kill_crops
## Manager NA NA
## user_1 NA NA
## user_2 NA NA
## user_3 NA NA
## user_4 NA NAAlthough a second call of gmse_apply has identical
initial conditions, because resource demographics (e.g., birth and
death) and agent decision making (e.g., policy generation and user
actions) is not deterministic, a slightly different result is obtained
below.
rand_eg_2 <- gmse_apply();
print(rand_eg_2);## $resource_results
## [1] 1092
##
## $observation_results
## [1] 907.0295
##
## $manager_results
## resource_type scaring culling castration feeding help_offspring
## policy_1 1 NA 64 NA NA NA
##
## $user_results
## resource_type scaring culling castration feeding help_offspring
## Manager 1 NA 0 NA NA NA
## user_1 1 NA 15 NA NA NA
## user_2 1 NA 15 NA NA NA
## user_3 1 NA 15 NA NA NA
## user_4 1 NA 15 NA NA NA
## tend_crops kill_crops
## Manager NA NA
## user_1 NA NA
## user_2 NA NA
## user_3 NA NA
## user_4 NA NATo make meaningful model inferences, it is often necessary to
replicate simulations under the same initial conditions to understand
the range of predicted outcomes for a particular set of parameter
values. This can be computationally intense, but it can also lead to a
more robust understanding of the range of dynamics that might be
expected within a system. Additionally, when parameter values are
unknown but believed to be important, replicate simulations can be
applied across a range of values to understand how a particular
parameter might affect system dynamics. Below, we show how to use the
gmse_replicates function to simulate a simple example of a
managed population that is hunted by users. This function calls
gmse multiple times and aggregates the results from
replicate simulations into a single table.
For a single simulation, the gmse_table function prints
out key information from a gmse simulation result. The
example provided in the GMSE documentation is
below.
gmse_sim <- gmse(time_max = 10, plotting = FALSE);## [1] "Initialising simulations ... "
sim_table <- gmse_table(gmse_sim = gmse_sim);
print(sim_table)## time_step resources estimate cost_culling cost_unused act_culling
## [1,] 1 1123 1156.463 66 44 60
## [2,] 2 1214 1133.787 35 75 112
## [3,] 3 1255 1337.868 14 96 284
## [4,] 4 1132 952.381 110 0 36
## [5,] 5 1320 1269.841 18 92 220
## [6,] 6 1437 1700.680 10 100 400
## [7,] 7 1240 1247.166 19 91 208
## [8,] 8 1245 1315.193 14 96 284
## [9,] 9 1158 952.381 108 0 36
## [10,] 10 1343 1428.571 11 99 360
## act_unused harvested
## [1,] 2 60
## [2,] 3 112
## [3,] 0 284
## [4,] 3 36
## [5,] 1 220
## [6,] 0 400
## [7,] 0 208
## [8,] 0 284
## [9,] 1 36
## [10,] 0 360The above table can be saved as a CSV file using the
write.csv function.
write.csv(x= sim_table, file = "file_path/gmse_table_name.csv");Instead of recording all time steps in the simulation, we can instead
record only the last time step in gmse_table using the
all_time argument.
sim_table_last <- gmse_table(gmse_sim = gmse_sim, all_time = FALSE);
print(sim_table_last)## time_step resources estimate cost_culling cost_unused act_culling
## 10.000 1343.000 1428.571 11.000 99.000 360.000
## act_unused harvested
## 0.000 360.000The gmse_replicates function replicates multiple
simulations replicates times under the same initial
conditions, then returns a table showing the values of all simulations.
This can be useful, for example, for testing how frequently a population
is expected to go to extinction or carrying capacity under a given set
of parameter values. First, we demonstrate the
gmse_replicates function for simulations of up to 20 time
steps. The gmse_replicates function accepts all arguments
used in gmse, and also all arguments of
gmse_table (all_time and
hide_unused_options) to summarise multiple
gmse results. Here we use default gmse values
in replicate simulations, except plotting, which we set to
FALSE to avoid plotting each simulation result. We run 10
replicates below.
gmse_reps1 <- gmse_replicates(replicates = 10, time_max = 20, plotting = FALSE);
print(gmse_reps1);## time_step resources estimate cost_culling cost_unused act_culling
## [1,] 20 987 816.3265 110 0 36
## [2,] 20 1160 1111.1111 42 68 92
## [3,] 20 1096 1179.1383 27 83 148
## [4,] 20 895 1065.7596 72 38 52
## [5,] 20 1197 1201.8141 24 86 164
## [6,] 20 1281 1587.3016 10 100 400
## [7,] 20 1284 952.3810 108 1 36
## [8,] 20 1124 1156.4626 30 80 132
## [9,] 20 1429 1791.3832 10 100 400
## [10,] 20 1227 1088.4354 54 56 72
## act_unused harvested
## [1,] 1 36
## [2,] 6 92
## [3,] 0 148
## [4,] 12 52
## [5,] 2 164
## [6,] 0 400
## [7,] 2 36
## [8,] 0 132
## [9,] 0 400
## [10,] 6 72Note from the results above that resources in all simulations
persisted for 20 time steps, which means that extinction never occurred.
We can also see that the population in all simulations never terminated
at a density near the default carrying capacity of
res_death_K = 2000, and was instead consistently near the
target population size of manage_target = 1000. If we wish
to define management success as having a population density near target
levels after 20 time steps (perhaps interpreted as 20 years), then we
might assess this population as successfully managed under the
conditions of the simulation. We can then see what happens if managers
only respond to changes in the social-ecological system with a change in
policy once every two years, perhaps as a consequence of reduced funding
for management or increasing demands for management attention elsewhere.
This can be done by changing the default manage_freq = 1 to
manage_freq = 2.
gmse_reps2 <- gmse_replicates(replicates = 10, time_max = 20, plotting = FALSE,
manage_freq = 2);
print(gmse_reps2);## time_step resources estimate cost_culling cost_unused act_culling
## [1,] 20 1670 1814.0590 10 100 400
## [2,] 20 1416 1383.2200 12 98 332
## [3,] 20 1156 1315.1927 15 95 264
## [4,] 20 1171 1088.4354 53 57 72
## [5,] 20 1241 1519.2744 10 100 400
## [6,] 20 1500 1405.8957 12 98 332
## [7,] 20 1263 907.0295 110 0 36
## [8,] 20 1399 1632.6531 10 100 400
## [9,] 20 1287 1451.2472 10 100 400
## [10,] 20 906 884.3537 110 0 36
## act_unused harvested
## [1,] 0 400
## [2,] 0 332
## [3,] 1 264
## [4,] 10 72
## [5,] 0 400
## [6,] 0 332
## [7,] 2 36
## [8,] 0 400
## [9,] 0 400
## [10,] 2 36Note that while extinction still does not occur in these simulations,
when populations are managed less frequently, they tend to be less close
to the target size of 1000 after 20 generations. The median population
size of gmse_reps1 (management in every time step) was
1178.5, with a maximum of 1429 and minimum of 895. The median population
size of the newly simulated gmse_reps2 (management every
two time steps) is 1275, with a maximum of 1670 and minimum of 906. We
can now see what happens when management occurs only once in every three
time steps.
gmse_reps3 <- gmse_replicates(replicates = 10, time_max = 20, plotting = FALSE,
manage_freq = 3);
print(gmse_reps3);## time_step resources estimate cost_culling cost_unused act_culling
## [1,] 20 1153 839.0023 110 0 36
## [2,] 20 996 1541.9501 10 100 400
## [3,] 20 1035 1156.4626 30 80 132
## [4,] 20 613 1632.6531 10 100 400
## [5,] 20 964 793.6508 110 0 36
## [6,] 20 709 544.2177 109 1 36
## [7,] 20 1292 884.3537 110 0 36
## [8,] 20 1438 907.0295 110 0 36
## [9,] 20 700 476.1905 109 0 36
## [10,] 20 1157 1247.1655 18 92 220
## act_unused harvested
## [1,] 1 36
## [2,] 0 400
## [3,] 2 132
## [4,] 0 400
## [5,] 0 36
## [6,] 1 36
## [7,] 2 36
## [8,] 2 36
## [9,] 3 36
## [10,] 4 220Given a management frequency of once every three time steps, the
median population size of gmse_reps3 (management in every
time step) is 1015.5, with a maximum of 1438 and minimum of 613. The
number of extinctions observed in these replicate populations was 0.
Below we change the management frequency to once every four time
steps.
gmse_reps4 <- gmse_replicates(replicates = 10, time_max = 20, plotting = FALSE,
manage_freq = 4);
print(gmse_reps4);## time_step resources estimate cost_culling cost_unused act_culling
## [1,] 5 0 0.00000 110 0 36
## [2,] 8 0 0.00000 110 0 36
## [3,] 4 0 0.00000 110 0 36
## [4,] 5 0 90.70295 110 0 36
## [5,] 6 0 45.35147 109 1 36
## [6,] 9 0 0.00000 110 0 36
## [7,] 4 0 0.00000 110 0 36
## [8,] 5 0 22.67574 110 0 36
## [9,] 6 1 68.02721 110 0 36
## [10,] 4 0 0.00000 110 0 36
## act_unused harvested
## [1,] 1 0
## [2,] 2 0
## [3,] 1 0
## [4,] 2 0
## [5,] 3 0
## [6,] 2 0
## [7,] 1 0
## [8,] 1 0
## [9,] 1 1
## [10,] 3 0Now note from the first column of gmse_reps4 above that
10 populations did not persist to the 20th time step; i.e., 10
populations went to extinction (note that GMSE has a minimum resource
population size of 5). This has occured because managers cannot respond
quickly enough to changes in the population density, and therefore
cannot increase the cost of culling to maintain target resource levels
if population size starts to decrease. We can see the extinction risk
increase even further if management only occurs once every 5 time
steps.
gmse_reps5 <- gmse_replicates(replicates = 10, time_max = 20, plotting = FALSE,
manage_freq = 5);
print(gmse_reps5);## time_step resources estimate cost_culling cost_unused act_culling
## [1,] 4 0 1000 0 -10 400
## [2,] 5 0 0 109 1 36
## [3,] 5 0 0 110 0 36
## [4,] 4 0 1000 0 -10 400
## [5,] 4 0 1000 0 -10 400
## [6,] 5 0 0 110 0 36
## [7,] 5 0 0 110 0 36
## [8,] 4 0 1000 0 -10 400
## [9,] 5 0 0 110 0 36
## [10,] 5 0 0 110 0 36
## act_unused harvested
## [1,] 0 0
## [2,] 1 0
## [3,] 0 0
## [4,] 0 0
## [5,] 0 0
## [6,] 2 0
## [7,] 1 0
## [8,] 0 0
## [9,] 2 0
## [10,] 1 0When a manager can only make policy decisions once every five time
steps, extinction occurs in 10 out of 10 simulated populations before
year 20. If we wanted to summarise these results, we could plot how
extinction risk changes with increasing manage_freq.
ext_risk1 <- sum(gmse_reps1[,2] < 20);
ext_risk2 <- sum(gmse_reps2[,2] < 20);
ext_risk3 <- sum(gmse_reps3[,2] < 20);
ext_risk4 <- sum(gmse_reps4[,2] < 20);
ext_risk5 <- sum(gmse_reps5[,2] < 20);
y_var <- c(ext_risk1, ext_risk2, ext_risk3, ext_risk4, ext_risk5);
x_var <- 1:5;
plot(x = x_var, y = y_var, type = "b", pch = 20, lwd = 2, cex = 1.5,
xlab = "Management every N time steps (manage_freq)",
ylab = "Freq. of population extinction", cex.lab = 1.25)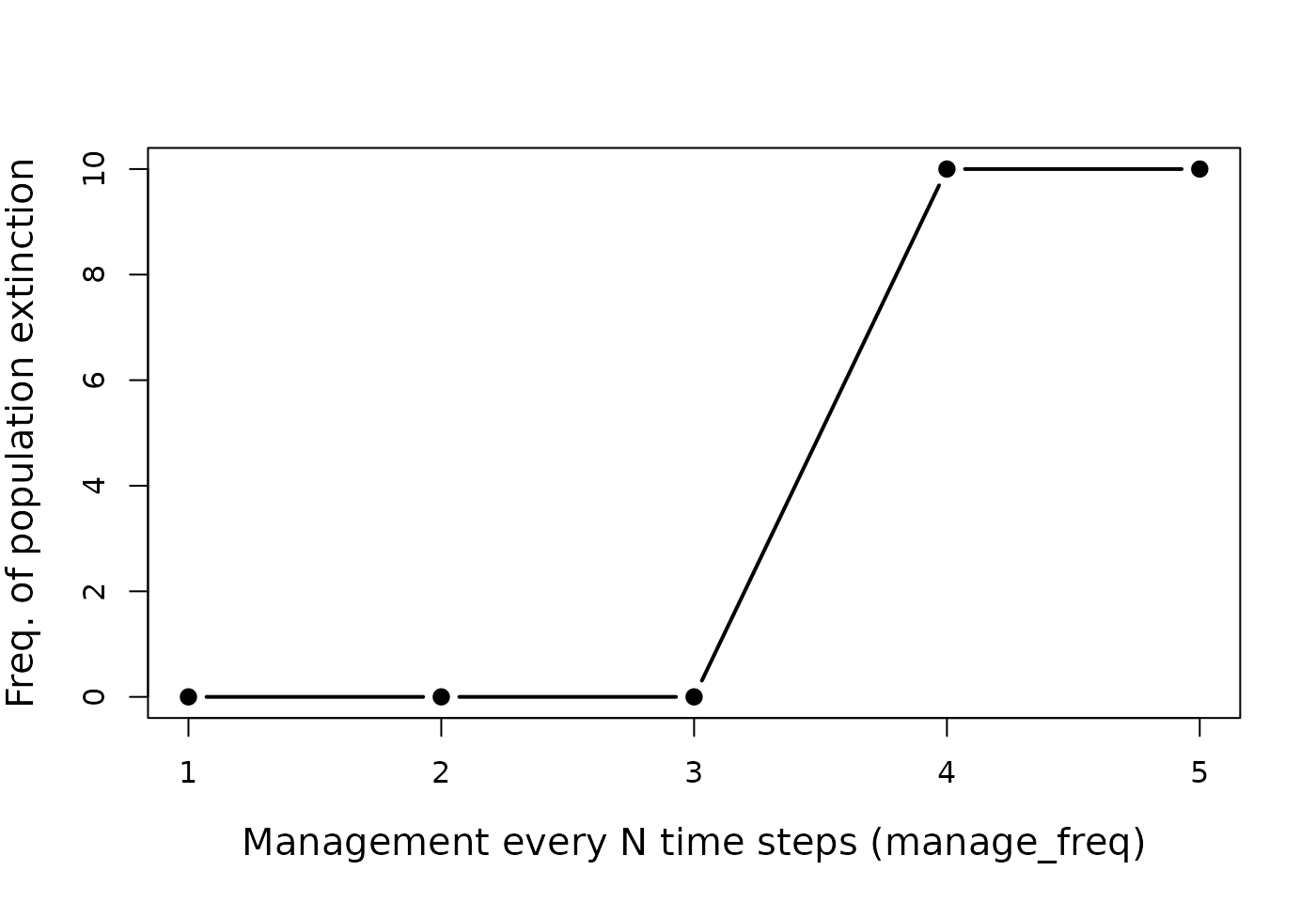
Extinction risk given an increasing number of time steps between updating policy decisions for culling costs in a simulated population. Higher values on the x-axis correspond to more time passing before a new policy is set. For each point, a total of 10 replicate simulations were run.
The above plot and the simulations from which it was derived illustrates a greatly simplified example of how GMSE might be used to assess the risk of extinction in a managed population. A comprehensive analysis would need more than 10 replicate simulations to accurately infer extinction risk, and would require careful pararmeterisation of all sub-models and a sensitivity analysis where such parameters are unknown. A benefit of this approach is that it allows for the simulation of multiple different scenarios under conditions of uncertainty and stochasticity, modelling the range of outcomes that might occur within and among scenarios and facilitating the development of social-ecological theory. Future expansion on the complexity of individual-based default sub-models of GMSE will further increase the realism of targeted case studies.